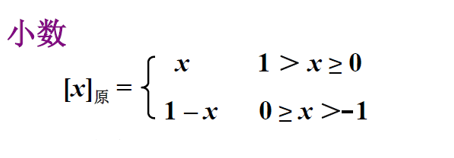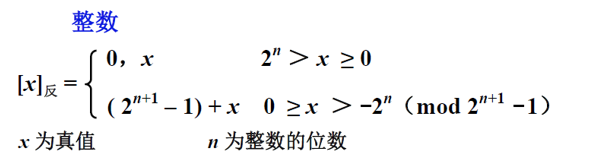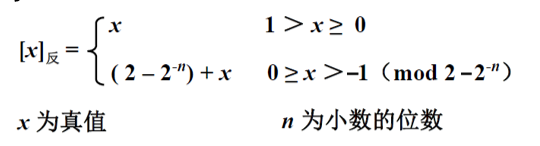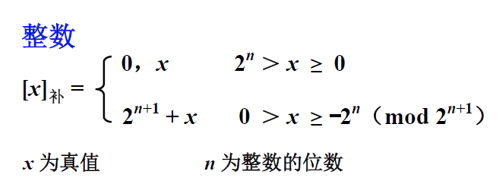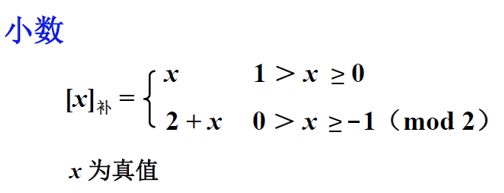数制转换

数制，也称为“计数制”，是用一组固定的符号和统一的规则来表示数值的方法。任何一个数制都包含两个基本要素：基数和位权。不同的数制可以进行进制转换。

🚪传送门：在线进制转换

数制

虽然计算机能极快地进行运算，但其内部并不像人类在实际生活中使用的十进制，而是使用只包含0和1两个数值的二进制。当然，人们输入计算机的十进制被转换成二进制进行计算，计算后的结果又由二进制转换成十进制，这都由操作系统自动完成，并不需要人们手工去做，学习汇编语言，就必须了解二进制（还有八进制/十六进制）。

重要概念

基数

R进制中只允许出现0，1，2…….R-1共R个数码，数码既可以是数，也可以是吗（如字母），则R就称为R进制的基数。

位权

R进制中，不同位置的1所表示的值不同，位号为i的1表示R^i，R^i称为位权。

进制规则

进位规则是指何种情况下向高位进位。R进制中，对位加法满R就应向高位进位，即逢R进一。

数制的相互转换

十进制转二进制：整数部分除基数（2）取余，小数部分乘基数（2）取整。

十进制转八进制：整数部分除基数（8）取余，小数部分乘基数（8）取整。

十进制转十六进制：整数部分除基数（16）取余，小数部分乘基数（16）取整。

其他进制转十进制：二进制，八进制，十六进制转十进制按权相加。

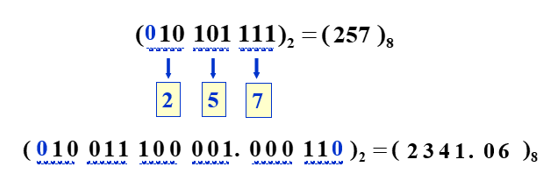
二进制转八进制：三位分一组，每三位进制数相当于一位8进制数。

八进制转二进制：每位八进制数转换为相应的三位二进制数。

二进制转十六进制：四位分一组，每四位二进制数相当于一位十六进制数。

十六进制转二进制：每位十六进制数转换为相应四位二进制数。

常见的一些数值表示及用法

1. （100…0）2 = 2N：表示 1 后面有 N 个 0 的二进制整数。
2. （111…1）2 = 2N+1-1：表示共有 N+1 个 1 的二进制整数。
3. （0.0…01）2 = 2-N：表示小数点后共有N-1 个 0 的二进制纯小数。
4. （0.1…11）2 = 1-2-N：表示 小数点后共有N 个 1 的二进制纯小数。
5. （111…1）2 -（X1X2…XN）2 = （X1X2…XN）2：表示共有N 个 1 的二进制整数减去一个N 位的二进制整数，结果是将减数按位取反。
6. （0.111…1）2 -（0.X1X2…XN）2 = （0.X1X2…XN）2：表示共有 N 个 1 的二进制纯小数减去一个小数部分有N 位的二进制纯小数，结果是将减数的小数部分按位取反。
7. ​ 二进制数左移K 位，相当于这个数乘以 2K。
8. ​ 二进制数右移K 位，相当于这个数除以

数值数据描述

无符号数和有符号数

无符号数（unsigned）

• 数据与数值相等，数据本身的N+1个二进制比特位全部用来表示其数值，没有符号位。
• 通常用于表示地址，作为计数器等用途。
• 范围[0，2^(N+1) -1]

有符号数（signed）

有符号数的数据分为符号和数值两个部分，N+1位有符号数的二进制比特位最左一位用于表示符号，其余N位用于表示数值。有符号数中涉及两个概念：真值 和 机器数。真值是带符号的数，即平时生活中数的表达方式。机器数是有符号数的数值化后在计算机存储中的数，是一个0、1序列。

1. 符号的数值化：+用0表示，-用1表示。
2. 数值编码：多种方案，如源码，反码，补码，移码等。
3. 小数点的表示：隐藏，不表示出来，只是事先约定好即可。

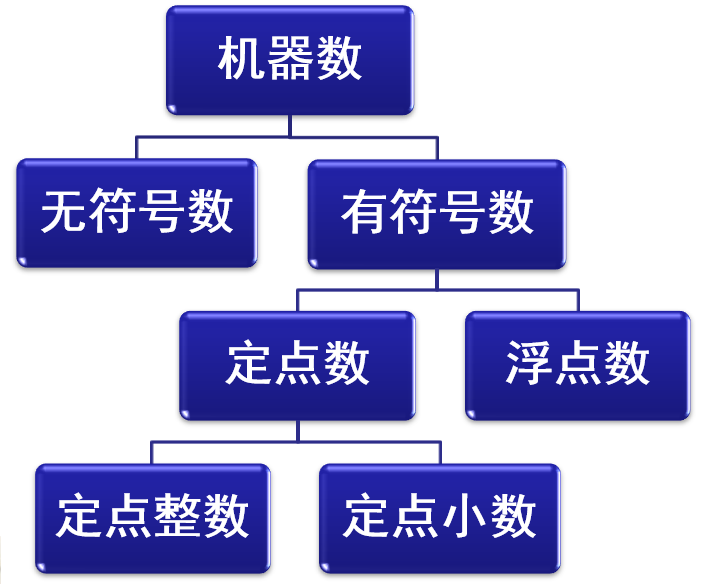
定点数和浮点数

定点数的表示

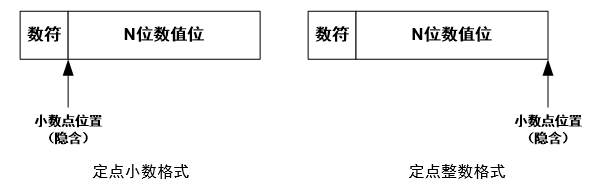
小数点固定在某一位置的数为定点数，有两种格式，当小数点位于数符和第一数值位之间时，计算机内的数位纯小数；当小数点位于数值最后时，计算机内的数位纯整数。采用定点的计算叫做定点机，数值部分的位数N决定了定点机种数的表示范围。在定点机中，由于小数点的位置固定不变，故当计算机处理的数不是纯小数或纯整数时，必须乘上一个比例因子，否则会产生“溢出”。

浮点数的表示

实际上计算机中处理的数不一定是纯小数或纯整数，因此都不能直接用定点小数或定点整数表示，所以要用浮点数表示。

• 浮点数即小数点的位置可以浮动的数。
• 将尾数最高位为1的浮点数称作规格化数。
• 左规与右规。

浮点数的表示形式

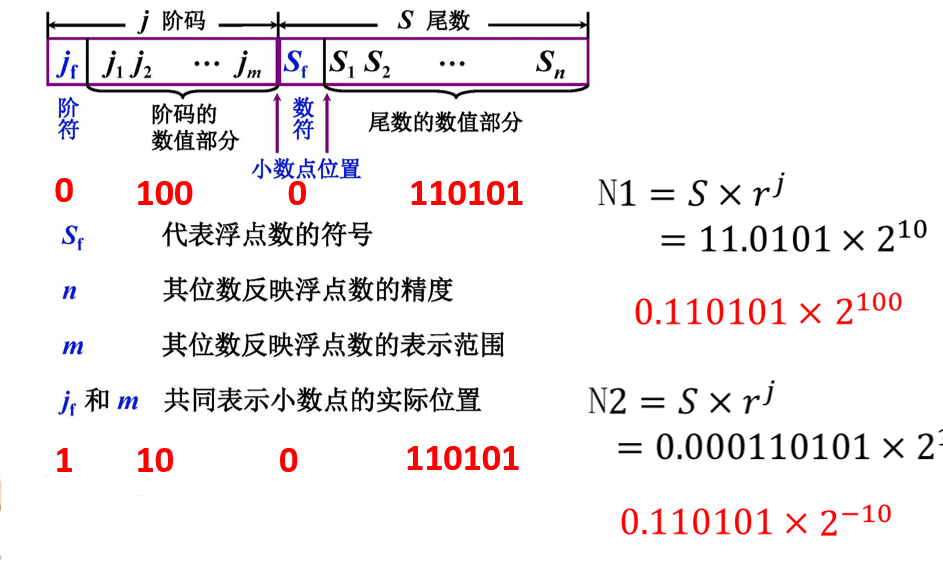
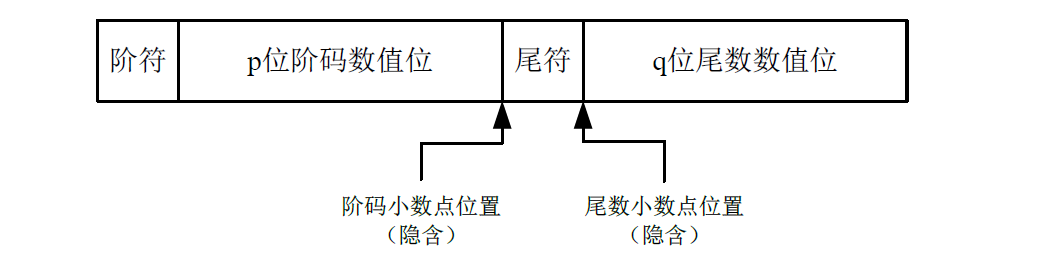
浮点数在计算机中的形式如图 所示，采用这种数据格式的计算机叫做浮点机。浮点数由阶码和尾数两部分组成。阶码是整数，阶符和阶码的位数 p+1 合起来反映浮点数的表示范围及小数点的实际位置；尾数是小数，其位数反映了浮点数的精度；尾数的符号代表浮点数的正负。

浮点数的规格化

为了提高浮点数的精度，其尾数必须为规格化数。如果不是规格化数，就要通过修改阶码并同时左右移尾数的办法，使其变成规格化数。将非规格化数转换成规格化数的过程叫做规格化。对于基数不同的浮点数，因其规格化数的形式不同，规格化过程也不同。

当基数为 2 时，尾数采用带符号的二进制数表示时，尾数最高数值位为 1 的数为规格化数。规格化时， 尾数左移一位，阶码减 1，这种规格化叫做向左规格化，简称左规；尾数右移一位，阶码加 1，这种规格化叫做向右规格化，简称右规。

浮点机中基数一旦确定就不再变了，而且基数是隐含的，故不同基数的浮点数其表示形式完全相同。但基数不同，对数的表示范围和精度等都受影响。一般来说，基数R 越大，可表示的浮点数范围越宽，而且所表示的数其个数越多。但R 越大，浮点数的精度反而下降。如 R=16 的浮点数，因其规格化数的尾数最高三位可能出现零，故与其尾数位数相同的 R=2 的浮点数相比，后者可能比前者多三位精度。

数值范围和数据精度

由于计算机硬件限制只能用有限的二进制比特位来表示数据（假定为 N+1 位），因此对于数值数据而言，计算机的数值数据不可能把所有的数（无论整数、小数还是一般意义的实数）都表示出来，从而存在它能够表示的数值范围和数据精度。这里需要注意的是只要提到二进制都会有这样一个问题，这个二进制数有多少位，这个位数将决定数值的范围和精度。一般情况下，在出现的数据运算中出现的任一个数都要保持这种位数，不能任意减少，更不能增加。关于数值范围和数据精度有以下几个概念。

• 数值范围：一种类型的数据所能表示的最大值和最小值。
• 数据精度：一种类型的数据所能表示的有效数据位的位数。
• 溢出：超出数据表示的范围称为溢出。
• 正溢：定点数中大于所能表示的最大正数。
• 负溢：定点数中小于所能表示的最小负数。

定点数的编码方案

假定用N+1个二进制比特来表示定点数，最左为符号位，右N位为数值位，定点数的表示方法为原码表示法、反码表示法和补码表示法。

原码

原码表示法把数值的绝对值转换成二进制以后在最高位加上其符号的数值表示，原数值的符号位+和-分别用0和1表示。

0的原码不唯一

需要注意的是 0 的编码有“+0”和“-0”的区别：[+0]原=00000000，[-0]原=10000000。也就是说，0 的原码不唯一。

反码

反码表示法对数的处理过程与数值的符号有关，如果为正数则其编码与原码相同；如果为负数把原码的符号位不变，其他位（数据位）取反。

0的反码不唯一

其中 0 的编码不一致的问题仍然存在，其编码为：[+0]反=00000000，[-0]反=11111111。0 的反码不唯一！

补码

补码表示法对数的处理过程与数值的符号有关，如果位正数则其编码与原码相同，如果位负数则在反码的最末位加上1，计算所得到的编码即为其的补码。

0的补码唯一

对 0 编码时，[+0]补=00000000，[-0]补=00000000。由此可见，0 的补码是唯一的！

补码的性质

已知[X]补，求[X]原、[-X]补、[2X]补、[X/2]补的方法。

• [X]原= [X]补（正数），[X]原= [[X]补]补（负数）
• [-X]补= [X]补连同符号位一起按位取反，末尾加1
• [2X]补= [X]补连同符号位一起左移一位，右边补0（符号位不能变）
• [X/2]补= [X]补连同符号位一起右移一位，左边补符号位（舍去）

变形补码

变形补码是实质是双符号位补码，只需要将补码的符号位多写一位即可。变形补码主要用于方便判断运算是否溢出。

移码

将一个数的补码的符号位取反所得的编码即为其移码。移码只用于表示定点整数。

移码中 0 的编码是：[+0]移=10000000，[-0]移=10000000。0 的移码表示是唯一的！

移码表示的整数可直接比较大小，通常用于表示浮点数的阶码，便于浮点数运算。

性质

• 最高位为符号位，书写上用,（整数）或.（小数）将数值部分和符号位隔开。
• 对于正数，原码 = 补码 = 反码 。
• 对于负数，符号位为1，（补码）其数值部分原码除符号位外每位取反末位加1；（反码）原码出符号位外每位取反。

例

假设机器字长为8，符号位取1位，数据位取7位，求+10和-10的原码、反码、补码、移码

	+10	-10
二进制形式	+000101	-0001010
原码	0 000101	1 0001010
反码	0 000101	1 1110101
补码	0 000101	1 1110110
移码	1 000101	0 1110110

假设机器字长为8，符号位取1位，数据位取7位，求+0.625和-0.625的原码、反码、补码

	+0.625	-0.625
二进制形式	+0.1010000	-0.1010000
原码	0.1010000	1.1010000
反码	0.1010000	1.0101111
补码	0.1010000	1.0110000

十进制数的编码

BCD码

用二进制代码来为十进制数编码，即是用若干位二进制的编码来表示进制的每一个数码0~9，一般用四位二进制来表示一位十进制，这样，就可以在只识别二进制的编码来表示计算机中利用十进制来表示的数值。

BCD码的编码方案

BCD码实质都是利用四位二进制来表示一位十进制数码，方案很多，按照其编码是否根据特定的权值构成，分为有权码和无权码。有权码有8421码、2421码和5421码等编码方式，通常用得最多的就是8421码，所以一般BCD如果不特殊说明就是指8421码。

无权码有余3码和格雷码等编码方式。余3码的编码方式就是在8424码的编码上加上3做数值计算得到的编码。格雷码的主要特点为任何两组相邻码子中只有一位二进制不同，它用多种编码方案。一种方案为8421码加一个前导0，然后相邻两位异或得到。

十进制数码	8421码	余3码	格雷码
0	0000	0011	0000
1	0001	0100	0001
2	0010	0101	0011
3	0011	0110	0010
4	0100	0111	0100
5	0101	1000	0111
6	0110	1001	0101
7	0111	1010	0100
8	1000	1011	1100
9	1001	1100	1101

文本数据描述

ASCLL码

🚪传送门： ascll码表在线查询

ASCII是由电报代码发展而来的。它的第一个商业用途是作为贝尔数据服务公司推广的七位电传打字机代码。ASCII标准的工作始于1960年10月6日，美国标准协会(ASA)(现为美国国家标准协会或ANSI) X3.2小组委员会的第一次会议。该标准的第一版于1963年出版， 在1967年进行了重大修订，并在1986年进行了最新更新。 与早期的电报代码相比，建议的贝尔代码和ASCII都是为了更方便地对列表进行排序(即按字母顺序排列)，并为电传打字机以外的设备增加了功能。
目前使用最广泛的英文字符集及其编码是ASCII 字符集和ASCII 码（ASCII 是 American Standard Code for Information Interchange 的缩写）， 它同时也被国际标准化组织（ International Organization for Standardization, ISO）批准为国际标准。
基本的 ASCII 字符集共有 128 个字符，其中有 96 个可打印字符，包括常用的字母、数字、标点符号等，另外还有 32 个控制字符。标准 ASCII 码使用 7 位二进制数对字符进行编码，对应的 ISO 标准为 ISO646 标准。

计算机基本处理单位为字节（1Byte=8bit），ASCLL码仍以一个字节来存放每，每一个字节中多出的一位（最高位）在计算机内部通常保持为0，可用于奇偶校验。

汉字的编码

汉字编码为汉字设计的一种便于输入计算机的代码。由于电子计算机现有的输入键盘与英文打字机键盘完全兼容。因而如何输入非拉丁字母的文字（包括汉字）便成了多年来人们研究的课题。汉字信息处理系统一般包括编码、输入、存储、编辑、输出和传输。根据应用目的的不同，汉字编码分为外码、交换码、机内码和字形码。

输入码

输入码也叫外码，是用来将汉字输入到计算机中的一组键盘符号。英文字母只有 26 个，可以把所有的字符都放到键盘上，而使用这种办法把所有的汉字都放到键盘上，是不可能的。所以汉字系统需要有自己的输入码体系，使汉字与键盘能建立对应关系。目前常用的输入码有拼音码、智能全拼输入法和五笔字型输入法。

交换码

计算机内部处理的信息，都是用二进制代码表示的，汉字也不例外。而二进制代码使用起来是不方便的，于是需要采用信息交换码。我国使用国标码，国标码字符集中收集了常用汉字和图形符号 7445 个，其中图
形符号 682 个，汉字 6763 个，按照汉字的使用频度分为两级，第一级为常用汉字 3755 个，第二级为次常用汉字 3008 个。为了避开 ASCII 字符中的不可打印字符 0100001-1111110（十六进制为 21-7E），国标码表示汉字的范围为 2121-7E7E（十六进制）。

区位码是国标码的另一种表现形式，把国标GB2312-80 中的汉字、图形符号组成一个 94×94 的方阵， 分为 94 个“区”，每区包含 94 个“位”，其中“区”的序号由 01 至 94，“位”的序号也是从 01 至 94。94 个区中
位置总数＝94×94 ＝8836 个，其中 7445 个汉字和图形字符中的每一个占一个位置后，还剩下 1391 个空位，
这 1391 个位置空下来保留备用。所以给定“区”值和“位”值，用四位数字就可以确定一个汉字或图形符号， 其中前两位是“区”号，后两位是“位”号。

• 01-15 区：是各种图形符号、制表符和一些主要国家的语言字母，其中 01–09 区为标准符号区，共有682 个常用符号。

• 10-15 区：为自定义符号区，可留作用户自己定义。

• 16-55 区：是一级汉字区，共有 3755 个常用汉字，以拼音为序排列。

• 56-87 区：是二级汉字区，共有 3008 个次常用汉字，以部首为序排列。

• 88-94 区：自定义汉字区，可留作用户自己定义。

机内码

每一个汉字确定的二进制代码，既把国标码的每一个字节的首位置1（为了解决和ASCLL码的冲突）。

字形码

汉字的输出码，输出汉字时都采用图形方式，无论汉字的笔画多少，每个汉字都可以写在同样大小的方块中。

区位码、国标码和汉字内码

汉字的区位码的区号和位号各占一个字节，区号和位号都是用十进制表示的。汉字的国标码是用 4 位
的十六进制数描述的。汉字在计算机内用两个字节存储，即汉字的内码是 16 位二进制，但是为了书写方便还是用十六进制。
汉字的机内码、国际码和区位码之间的关系是：
（汉字的十进制区号）D =（国标码的高两位）H –（20）H
（汉字的十进制位号）D =（国标码的低两位）H –（20）H
（汉字的内码）H = （国标码）H+ （8080）H
例 2.10：“啊”字的国标码为 3021H（可以参考GB2312-80 文档）。
它的区位码为 3021H – 2020H = 1001H，即它在第 16 区，第 01 位。它在计算机内部的存储的内码为：3021H + 8080H = B0A1H。

其他信息形式的表示

计算机内任何形式的信息最终都将转换为二进制数据进行存储，对于较复杂的信息形式都采用的各自领域的编码形式，也可以说成定义了不同的数据结构，使顺序的二进制数据不同部分表述不同意义。

图像

• BMP：位图格式
• GIF：图形交换格式
• JPEG：有损压缩格式

音频

• 采样率和采样大小

  • 采样的过程就是抽取某点的频率值
  • 采样率：采样的频率
  • 采样大小：采样频率的能量值并量化

• 有损与无损

  • 相对自然界的信号，任何数字音频编码方案都是有损的
  • PCM约定俗成了无损编码

• PCM编码：音质好，体积大

• WAVE：较高音质，音乐编辑创作的首选格式

视频

• FLC：无声时代
• AVI：音频视频交叉存取格式
• MPEG编码
• 流媒体：MPEG-4，便下载边播放

数据校验

计算机对数据进行传送、存储和操作的过程中，都有可能由于硬件故障、软件错误或信息干扰等原因而导致数据出错。为了有效地防止、减少或避免错码现象，就必须采取相应的技术手段来解决这个问题。校验码就是解决这一问题的主要手段。
数据进行传送、存储和操作的过程中可能出现的问题包括代码是否出错了、错在什么地方以及如何纠正。
校验码分为两类：一类为检错码，即检查代码是否出错，但不能确定何处出错，不能修改；另一类为纠错码，即不仅能检查出错误，还能定位错误并纠正。常用的校验码有奇偶校验码、海明码、循环冗余码CRC 等。

奇偶校验

奇偶校验码是奇校验码和偶校验码的统称，是一种最基本的检错码。奇偶校验码是由 n-1 位信息元和1 位校验元组成，可以表示成为（n，n-1）。如果是奇校验码，在附加上一个校验元以后，码长为 n 的码字中“1”的个数为奇数个；如果是偶校验码，在附加上一个校验元以后，码长为 n 的码字中“1”的个数为偶数个。

例 2.14：被校验的代码为 1000001，则奇偶校验码分别为

奇校验码：11000001 （最左位为校验位）

偶校验码：01000001 （最左位为校验位）

海明码

海明码是由 R.HmIMI1ing 在 1950 年首次提出的，它是一种可以纠正一位差错的编码。可以借用简单奇偶校验码的生成原理来说明海明码的构造方法。