定点加减
负数用补码表示后就可以和正数一样来处理。这样运算器里只需要一个加法器就可以了,不必为了负数的加法运算再配一个减法器
补码加法
公式
[X]补+[Y]补=[X+Y]补 (mod 2n+1)
任意两数的补码之和等于该数之和的补码
特点
- 符号位要作为数的一部分一起参与运算
- 要在模2n+1的意义下相加,即超过2n+1的进位要丢掉
例:x=+1001,y=+0101,求x+y
[X]补=01001 [Y]补=00101 (第一位是符号位)
[X+Y]补=X]补+[Y]补=01110
x+y=+1110 (正数去掉符号位,写上+)
例:x=+1001,y= -0101,求x+y
[X]补=01001 [Y]补=11011 (负数求补码,先求反码再末位加1)
[X+Y]补=X]补+[Y]补=00110 (1溢出)
x+y=+0110 (PS:正数去掉符号位,写上+)
补码减法
负数的加法要利用补码话为加法来做,减法运算也要设法化为加法来做。之所以使用这种方法而补使用直接减法,是因为它可以和常规的加法运算使用同一加法器电路,从而简化了计算机的设计。
公式
[X-Y]补=[X]补-[Y]补=[X补]+[-Y]补
[-Y]补= ~[Y]补+2-n (对Y的补码包括符号位在内取反再末位加1)
例:x=+1101,y=+0110,求x-y
[x]补=01101 [y]补=00110 [-y]补=11010
[x-y]补=[x]补+[-y]补=00111 (1溢出)
x-y= +0111
溢出
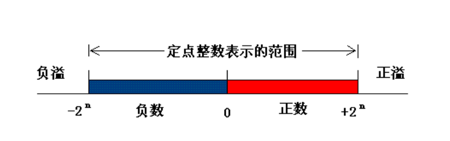
在定点机器中,数的表示范围|x|<2n-1。在运算过程中如出现大于字长绝对值的现象,称为溢出,在定点机中,运算过程中出现溢出时其结果是不正确的,故运算器必须能检测出溢出。
- 两个正数相加结果大于机器字长所能表示的最大正数,正溢出。
- 两个负数相加结果大于机器字长所能表示的最小负数,负溢出。
双位符号法(变形补码)
[X]变形补+[Y]变形补=[X+Y]变形补
[[X]变形补]变形补=[X]原
[X-Y]变形补=[X+(-Y)]变形补=[X]变形补+[-Y]变形补
| 运算结果的两位符号位 | 溢出情况 |
|---|---|
| 00 | 未发生溢出,结果是一个正数 |
| 11 | 未发生溢出,结果是一个负数 |
| 01 | 正溢出 |
| 10 | 负溢出 |
特征
- 两个符号位都要看做数码一样参与运算
- 两位数进行2n+2为模的加法,即最高符号位上产生的进位要丢掉
例:x=+1100,y=+1000,求 x+y
[X+Y]变形补=[X]变形补+[Y]变形补=001100+001000=010100 (前两位符号位)
两个符号位出现“01”,表示正溢出,即结果大于+2n
例:x=-1100,y=-1000,求x+y
[X+Y]变形补=[X]变形补+[Y]变形补=110100+111000=101100 (前两位符号位)
两个符号位出现“10”,表示负溢出,即结果小于-2n
单符号位法
当最高有效位产生进位而符号位无进位时,产生正溢;当最高有效位无进位而符号位有进位时,产生负溢。
- 符号位的进位判断溢出,最高数值位的进位叫做“进位入”记作Cn-1,数值最高位有进位,Cn-1=1,没有进位Cn-1=0。
- 符号位产生的进位叫做“进位出”,记作Cn。
V=Cn⊕Cn-1(异或)
| Cn | Cn-1 | V |
|---|---|---|
| 0 | 0 | 正数 |
| 1 | 1 | 负数 |
| 1 | 0 | 负溢 |
| 0 | 1 | 正溢 |
定点乘除
乘法
在定点计算机中,两个原码表示的数相乘的运算规则是:乘积的符号位由两数的符号位按异或运算得到,而乘积的数值部分则是两个正数相乘之积。
乘积符号的运算法则是:同号相乘为正,异号相乘为负。由于被乘数和乘数的符号组合只有四种情况(00,01,10,11),因此积的符号可按“异或”(按位加)运算得到。
例
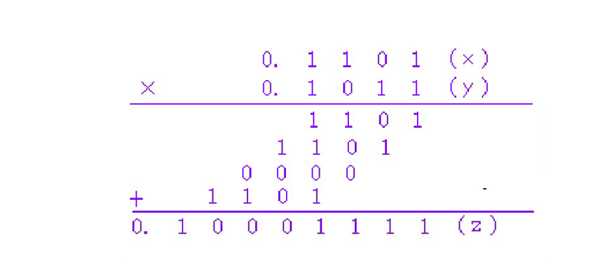
设x=0.1101,y=0.1011。(x是被乘数,y是乘数)
运算过程与十进制乘法相似:从乘数y的最低位开始,若这一位为“1”,则将被乘数x写下;若这一位为“0”,则写下全0。然后再对乘数y的高一位进行乘法运算,其规则同上一步,不过这一位乘数的权与最低位乘数的权不一样,因此被乘数x要左移一位。以此类推,直到乘数各位乘完为止,最后把它们统统加起来,便得到最后乘积。